前言

我們昨天說明了價值迭代方法，至此介紹完使用動態規劃，求解價值函數的方法。在進入另外兩個方法 (「蒙地卡羅方法」與「 TD learning」) 之前，我們先來回顧動態規劃方法的一些特色。

動態規劃方法 - 特色

更新所有狀態價值

不論是在 Policy Iteration 或是 Value Iteraiton 中，我們在更新狀態價值時，會更新所有的狀態。

• 優點
  更新所有狀態價值，是由價值函數的定義，衍伸出來的解決方案。因此滿足這個條件時，我們可以確保得到的狀態估計值，可以代表狀態價值，賦予這個數值意義。

• 缺點
  更新所有狀態價值，計算量會隨著狀態數量而改變。舉個例子來說，我們前面提到的 GridWorld 是一個 4x4 的世界，但如果我今天的世界大一點，是個 40x40 的世界。光是要更新狀態價值，我們就給花上 100 倍的時間，更何況我們不知需要更新狀態價值一次。另外，我們在處理的問題，也未必只有小維度 (ex: 二維、三維)

• 小結
  更新所有狀態價值，確保我們得到數值的意義，但也限制我們問題的大小。過於複雜的問題，可能不適合使用這個方法。事實上，這個限制來自於動態規劃本身，有興趣請見 Curse of dimensionality 。

• 額外討論
  那如果我們不更新狀態價值，會發生什麼事？
  從數學上來說，不更新所有狀態價值時，將不滿足價值函數定義。所以計算出來的出來的數值不一定代表真實的狀態價值，造成動作決策錯誤。

迭代輪流更新狀態價值與策略

在 Policy Iteration 中，使用 Policy Evalution 與 Policy Improvement 更新狀態價值，以及採取的策略。在 Value Iteration 中，其實也只是把兩個步驟合併為一個，並沒有少這個行為。

• 優點
  我們可以確保評估價值與策略，是往同一個方向、有相同目標。如下圖所示：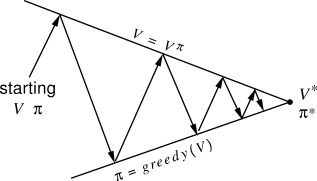
  

• 缺點
  透過迭代更新，代表我們必須不斷與環境互動，以更新價值狀態與策略。想像以下情境

  針對同一個問題，現在有三個人同時處理，我們可以得到三人的狀態價值與策略。

  雖然我們獲得其他三人的資訊，但我們卻沒法統整這些資訊 (ex: 評估誰的資訊比較好)，產生一個更準確的狀態價值或策略。因為你不知道那個人與環境互動到什麼程度了。說簡單一點，這個方法沒辦法分工。

• 小結
  迭代輪流更新狀態價值與策略，確保我們評估狀態價值和策略有相同的目標，這個過程讓我們限制沒辦法分工處理問題。

動態規劃方法 - 小結

以上，說明一些這個方法的特色。整體看來，動態規劃方法比較適合少量狀態的問題。除了動態規劃會遇到的 Curse of Dimensionality 外，沒辦法分工在處理複雜問題時會很麻煩。

至此，我們介紹完動態規劃方法，明天會開始介紹蒙地卡羅方法。